Queueing Theory - Part 1: A Study That Began in 1909 and Remains Essential Today

Have you ever wondered why there are entire studies dedicated to understanding queues? Whether waiting in line at the supermarket or troubleshooting performance issues in a software system, queues play a crucial role in both our daily experiences and complex technological infrastructures.

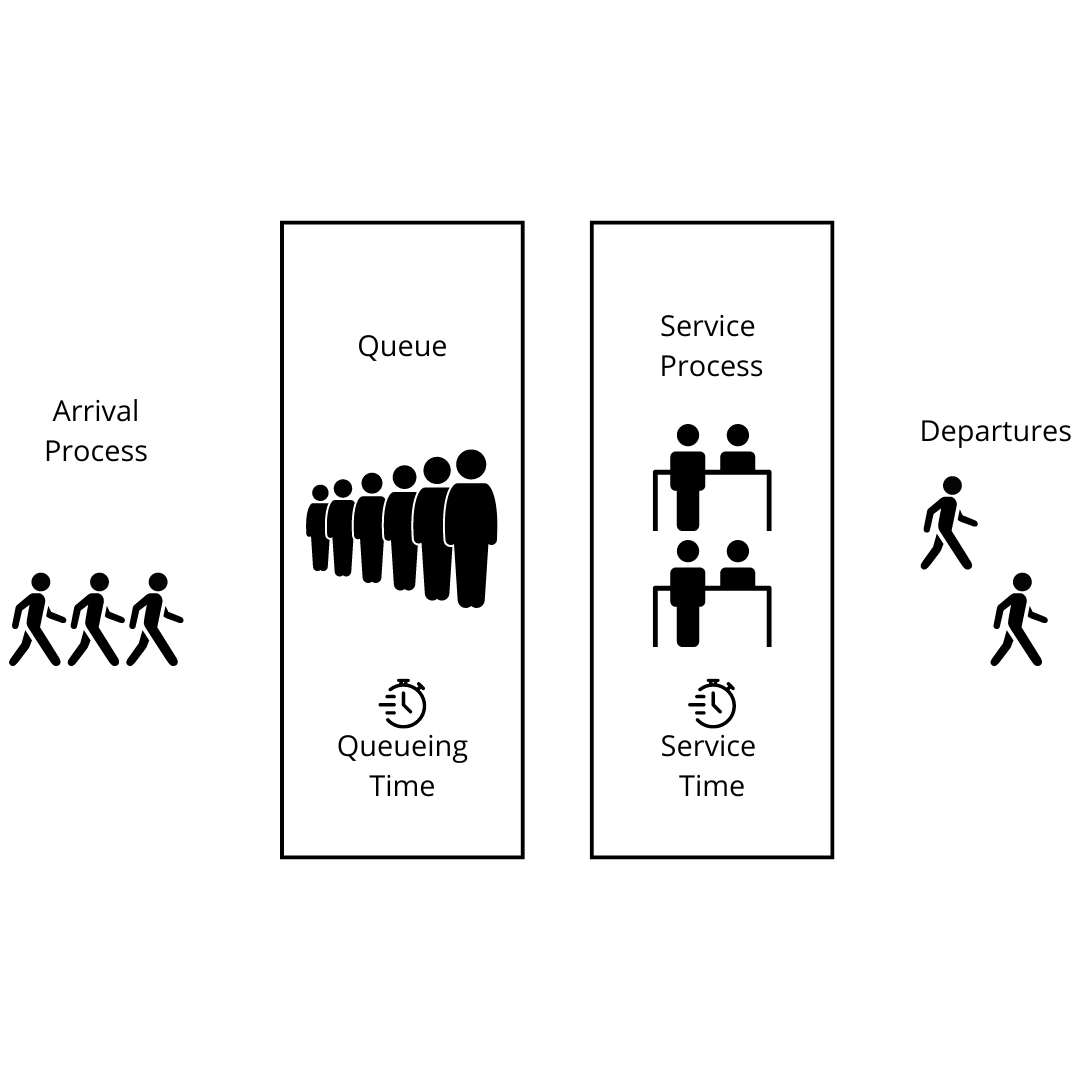
Queueing theory, a mathematical study of waiting lines, originated from the work of Agner Krarup Erlang, who developed models to understand how phone calls were handled at the Copenhagen Telephone Exchange. Today, the applications of queueing theory span far beyond telecommunications. It’s used in fields like traffic engineering, computing, project management, and industrial engineering to design more efficient systems and solve problems related to time, resources, and productivity.

---

Where Queueing Theory Shows Up in Everyday Life and Technology

In computing, queues manage everything from CPU tasks to requests in operating systems. Software applications also use queues to manage processes efficiently. Have you noticed how your computer prioritizes certain tasks over others, like responding to your keystrokes while processing background tasks? That’s queueing theory in action!

In project management, methodologies like Kanban rely on queueing theory to track work progress and prioritize tasks, helping teams optimize workflows and reduce bottlenecks. The study of queues is an integral part of management science, allowing organizations to use scientific methods to streamline operations.

---

Key Concepts in Queueing Theory

Queueing analysis is built around calculating operating characteristics—essentially the probabilities and averages that describe how queues behave. These include:

• The probability of a certain number of customers (or requests) being in the system.
• The average number of customers in the system or in the waiting line.
• The average time a customer spends waiting or being served.
• The probability that the server (whether human or machine) is busy or idle.

These characteristics help decision-makers improve the efficiency of queues, leading to reduced waiting times, better resource utilization, and cost savings.

---

1. Utilization (ρ)

Utilization tells you how busy the server is. It’s calculated as:

$\rho \; =\; \lambda \; /\; \mu$

Where:

• λ = average arrival rate (tasks per unit of time)
• μ = average service rate (tasks the server can handle per unit of time)

Interpretation:

• If ρ approaches 1, the server is very busy, which could result in long queues.
• If ρ is much lower than 1, the server is underutilized, indicating there may be excess capacity.

2. Average Number of Customers in the System (L)

The average number of customers (or tasks) in the system includes both tasks waiting in the queue and those being served. For an M/M/1 system (single server, Poisson arrivals, exponential service times), it can be calculated as:

$L\; =\; \rho \; /\; (1\; -\; \rho )$

Interpretation: This tells you how many tasks are present, on average, in the system (both in the queue and being processed).

3. Average Queue Length (Lq)

The average queue length gives you the expected number of customers waiting to be served. It can be calculated as:

$Lq\; =\; \rho ²\; /\; (1\; -\; \rho )$

Interpretation: It indicates how long the queue is, on average, which helps assess congestion.

4. Average Waiting Time in the System (W)

The average time a task spends in the system (both in the queue and being served) is calculated as:

$W\; =\; 1\; /\; (\mu \; -\; \lambda )$

Interpretation: It provides the average total time a task will spend from arrival to completion.

5. Average Waiting Time in the Queue (Wq)

The average waiting time in the queue specifically measures the time spent waiting to be served (excluding service time). It is calculated as:

$Wq\; =\; \rho \; /\; (\mu \; -\; \lambda )$

Interpretation: This tells you how long tasks wait in line before being processed, helping to identify potential delays.

6. Server Idle Time (1 - ρ)

The idle time of the server can be calculated as:

 Idle Time = 1 - ρ 

Interpretation: This metric helps to identify how often the server is idle and not processing tasks. High idle time indicates underutilization.

7. Response Time

Response time is the total time a task spends from arrival until completion (including waiting and service time). For an M/M/1 system, it can be approximated by:

$R\; =\; W\; =\; 1\; /\; (\mu \; -\; \lambda )$

Interpretation: It tells you how long, on average, a task will take from the moment it enters the queue until it leaves the system.

---

Applications

• System Scaling: Use utilization (ρ) and queue length (Lq) to decide whether additional servers or resources are required.
• Performance Bottlenecks: If waiting times (Wq) are high, the system might need optimization or additional capacity.
• Predicting Delays: Use average waiting time (W) and response time (R) to predict user delays and adjust resources accordingly.
• Load Balancing: Adjust workloads and priorities based on queue length and server utilization to maintain efficiency.

---

Queueing Theory in Action: Troubleshooting and Optimization

Queueing theory becomes especially valuable when you’re facing performance issues, scalability challenges, or bottlenecks. Here are key areas where it shines:

1. Identifying Bottlenecks

Queueing models can reveal where delays are happening in your system. Is it your CPU that’s overwhelmed? Or perhaps your database? By analyzing queue lengths and wait times, you can spot the exact point of failure and decide if adding resources or redistributing the load will help.

2. Addressing Scalability Issues

When your system struggles during peak times, queueing analysis can guide you in scaling up. Whether it’s adding servers, optimizing your code, or balancing the load more effectively, queueing models provide a framework for understanding how to grow sustainably.

3. Performance Tuning

Fine-tuning system performance often involves tweaking queues. For example, adjusting timeouts, prioritizing tasks, or implementing load-balancing strategies can drastically improve response times and overall system efficiency.

4. Task Prioritization

If some tasks are more critical than others, queueing theory helps you set up priority queues. In a web application, for instance, user interactions might take precedence over background tasks to ensure smooth experiences.

5. Proactive Monitoring

Using queueing theory for system monitoring allows you to set up alerts for key characteristics like queue length and server utilization. This way, you can address issues before they escalate into critical failures.

6. Capacity Planning and Failure Scenarios

Queueing theory aids in capacity planning by predicting how your system will perform as demand increases. It also helps simulate and prepare for failure scenarios, so you know exactly how to respond when resources fail.

7. Continuous Improvement

Finally, queueing theory promotes continuous refinement through feedback loops. By regularly analyzing real-world data, you can fine-tune your system to stay efficient as conditions evolve.

---

Conclusion: Why Queueing Theory Matters

Understanding queueing theory is crucial during system architecture, performance monitoring, and troubleshooting. Whether you're dealing with slowness, scalability, or inefficiencies, queueing theory provides the tools to identify issues, improve resource allocation, and optimize systems for peak performance.

Published on October 19, 2024